Econ 425T / Biostat 203B
Display system information for reproducibility.
import IPython
print(IPython.sys_info()){'commit_hash': 'add5877a4',
'commit_source': 'installation',
'default_encoding': 'utf-8',
'ipython_path': '/Users/huazhou/opt/anaconda3/lib/python3.9/site-packages/IPython',
'ipython_version': '8.8.0',
'os_name': 'posix',
'platform': 'macOS-10.16-x86_64-i386-64bit',
'sys_executable': '/Users/huazhou/opt/anaconda3/bin/python3',
'sys_platform': 'darwin',
'sys_version': '3.9.12 (main, Apr 5 2022, 01:56:13) \n[Clang 12.0.0 ]'}sessionInfo()R version 4.2.2 (2022-10-31)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Big Sur ... 10.16
Matrix products: default
BLAS: /Library/Frameworks/R.framework/Versions/4.2/Resources/lib/libRblas.0.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.2/Resources/lib/libRlapack.dylib
locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
attached base packages:
[1] stats graphics grDevices utils datasets methods base
loaded via a namespace (and not attached):
[1] Rcpp_1.0.9 here_1.0.1 lattice_0.20-45 png_0.1-8
[5] withr_2.5.0 rprojroot_2.0.3 digest_0.6.29 grid_4.2.2
[9] jsonlite_1.8.0 magrittr_2.0.3 evaluate_0.15 rlang_1.0.6
[13] stringi_1.7.8 cli_3.4.1 rstudioapi_0.13 Matrix_1.5-1
[17] reticulate_1.27 rmarkdown_2.14 tools_4.2.2 stringr_1.4.0
[21] htmlwidgets_1.6.1 xfun_0.31 yaml_2.3.5 fastmap_1.1.0
[25] compiler_4.2.2 htmltools_0.5.4 knitr_1.39 Load some libraries.
# Load the pandas library
import pandas as pd
# Load numpy for array manipulation
import numpy as np
# Load seaborn plotting library
import seaborn as sns
import matplotlib.pyplot as plt
# Set font sizes in plots
sns.set(font_scale = 1.2)
# Display all columns
pd.set_option('display.max_columns', None)
# Load Tensorflow and Keras
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layerslibrary(keras)In this example, we train an MLP (multi-layer perceptron) on the MNIST data set. Achieve testing accuracy 98.11% after 30 epochs.
The MNIST database (Modified National Institute of Standards and Technology database) is a large database of handwritten digits (\(28 \times 28\)) that is commonly used for training and testing machine learning algorithms.
60,000 training images, 10,000 testing images.
Acquire data:
# Load the data and split it between train and test sets
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
# Training set
x_train.shape(60000, 28, 28)y_train.shape
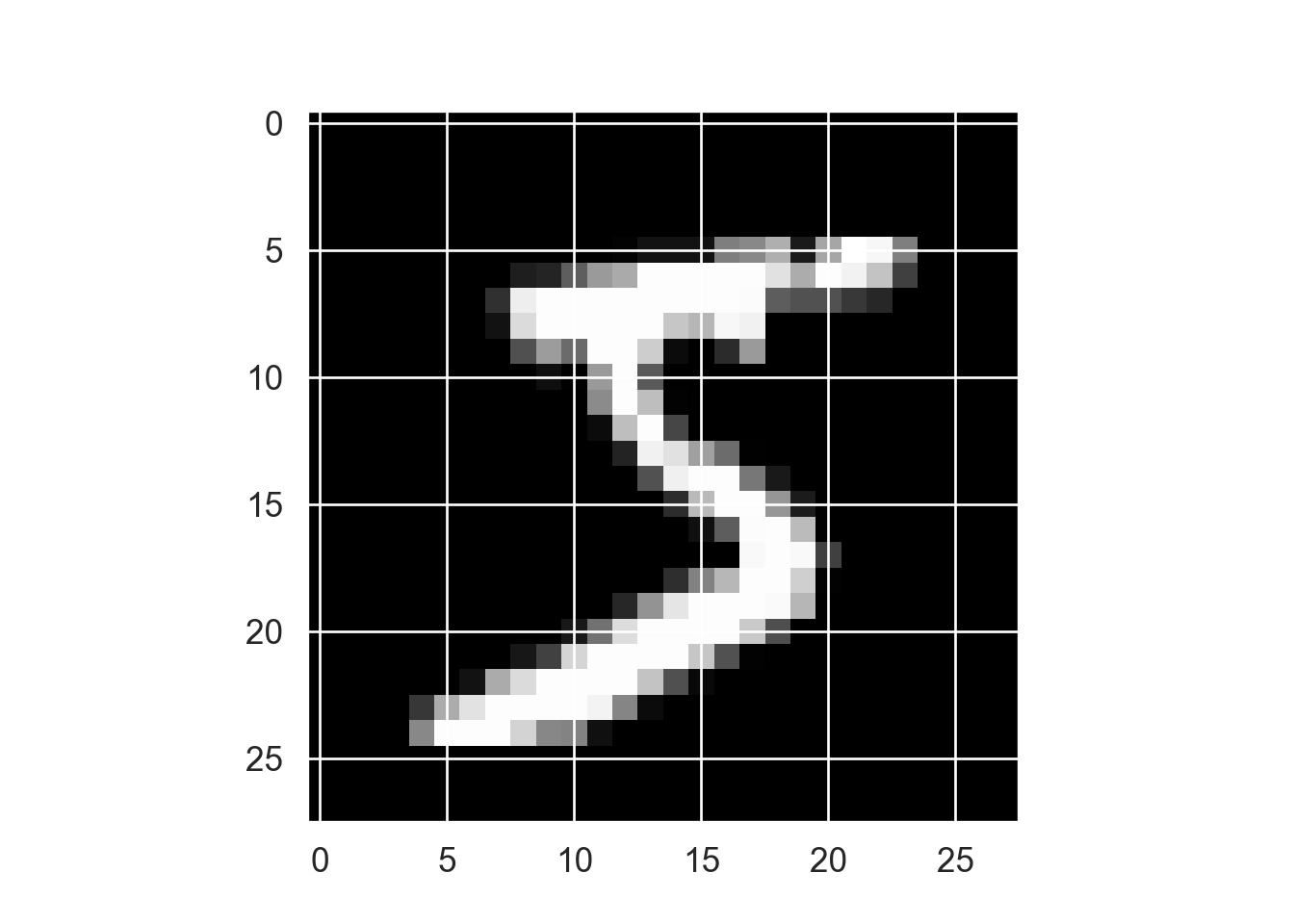
# Test set(60000,)x_test.shape(10000, 28, 28)y_test.shape(10000,)Display the first training instance and its label:
import matplotlib.pyplot as plt
# Feature: digit
plt.figure()
plt.gray()
plt.imshow(x_train[0]);
plt.show()
# Label
y_train[0]5mnist <- dataset_mnist()
x_train <- mnist$train$x
y_train <- mnist$train$y
x_test <- mnist$test$x
y_test <- mnist$test$yTraining set:
dim(x_train)[1] 60000 28 28dim(y_train)[1] 60000image(
t(x_train[1, 28:1,]),
useRaster = TRUE,
axes = FALSE,
col = grey(seq(0, 1, length = 256))
)
y_train[1][1] 5Testing set:
dim(x_test)[1] 10000 28 28dim(y_test)[1] 10000Vectorize \(28 \times 28\) images into \(784\)-vectors and scale entries to [0, 1]:
# Reshape
x_train = np.reshape(x_train, [x_train.shape[0], 784])
x_test = np.reshape(x_test, [x_test.shape[0], 784])
# Rescale
x_train = x_train / 255
x_test = x_test / 255
# Train
x_train.shape
# Test(60000, 784)x_test.shape(10000, 784)# reshape
x_train <- array_reshape(x_train, c(nrow(x_train), 784))
x_test <- array_reshape(x_test, c(nrow(x_test), 784))
# rescale
x_train <- x_train / 255
x_test <- x_test / 255
dim(x_train)[1] 60000 784dim(x_test)[1] 10000 784Encode \(y\) as binary class matrix:
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)
# Train
y_train.shape
# Test(60000, 10)y_test.shape
# First train instance(10000, 10)y_train[0]array([0., 0., 0., 0., 0., 1., 0., 0., 0., 0.], dtype=float32)y_train <- to_categorical(y_train, 10)
y_test <- to_categorical(y_test, 10)
dim(y_train)[1] 60000 10dim(y_test)[1] 10000 10head(y_train) [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 0 0 0 0 0 1 0 0 0 0
[2,] 1 0 0 0 0 0 0 0 0 0
[3,] 0 0 0 0 1 0 0 0 0 0
[4,] 0 1 0 0 0 0 0 0 0 0
[5,] 0 0 0 0 0 0 0 0 0 1
[6,] 0 0 1 0 0 0 0 0 0 0Define a sequential model (a linear stack of layers) with 2 fully-connected hidden layers (256 and 128 neurons):
model = keras.Sequential(
[
keras.Input(shape = (784,)),
layers.Dense(units = 256, activation = 'relu'),
layers.Dropout(rate = 0.4),
layers.Dense(units = 128, activation = 'relu'),
layers.Dropout(rate = 0.3),
layers.Dense(units = 10, activation = 'softmax')
]
)
model.summary()Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 256) 200960
dropout (Dropout) (None, 256) 0
dense_1 (Dense) (None, 128) 32896
dropout_1 (Dropout) (None, 128) 0
dense_2 (Dense) (None, 10) 1290
=================================================================
Total params: 235,146
Trainable params: 235,146
Non-trainable params: 0
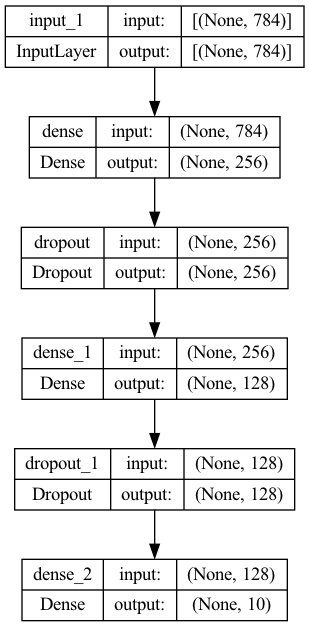
_________________________________________________________________Plot the model:
tf.keras.utils.plot_model(
model,
to_file = "model.png",
show_shapes = True,
show_dtype = False,
show_layer_names = True,
rankdir = "TB",
expand_nested = False,
dpi = 96,
layer_range = None,
show_layer_activations = False,
)
model <- keras_model_sequential()
model %>%
layer_dense(units = 256, activation = 'relu', input_shape = c(784)) %>%
layer_dropout(rate = 0.4) %>%
layer_dense(units = 128, activation = 'relu') %>%
layer_dropout(rate = 0.3) %>%
layer_dense(units = 10, activation = 'softmax')
summary(model)Model: "sequential_1"
________________________________________________________________________________
Layer (type) Output Shape Param #
================================================================================
dense_5 (Dense) (None, 256) 200960
dropout_3 (Dropout) (None, 256) 0
dense_4 (Dense) (None, 128) 32896
dropout_2 (Dropout) (None, 128) 0
dense_3 (Dense) (None, 10) 1290
================================================================================
Total params: 235,146
Trainable params: 235,146
Non-trainable params: 0
________________________________________________________________________________Compile the model with appropriate loss function, optimizer, and metrics:
model.compile(
loss = "categorical_crossentropy",
optimizer = "rmsprop",
metrics = ["accuracy"]
)model %>% compile(
loss = 'categorical_crossentropy',
optimizer = optimizer_rmsprop(),
metrics = c('accuracy')
)80%/20% split for the train/validation set.
batch_size = 128
epochs = 30
history = model.fit(
x_train,
y_train,
batch_size = batch_size,
epochs = epochs,
validation_split = 0.2
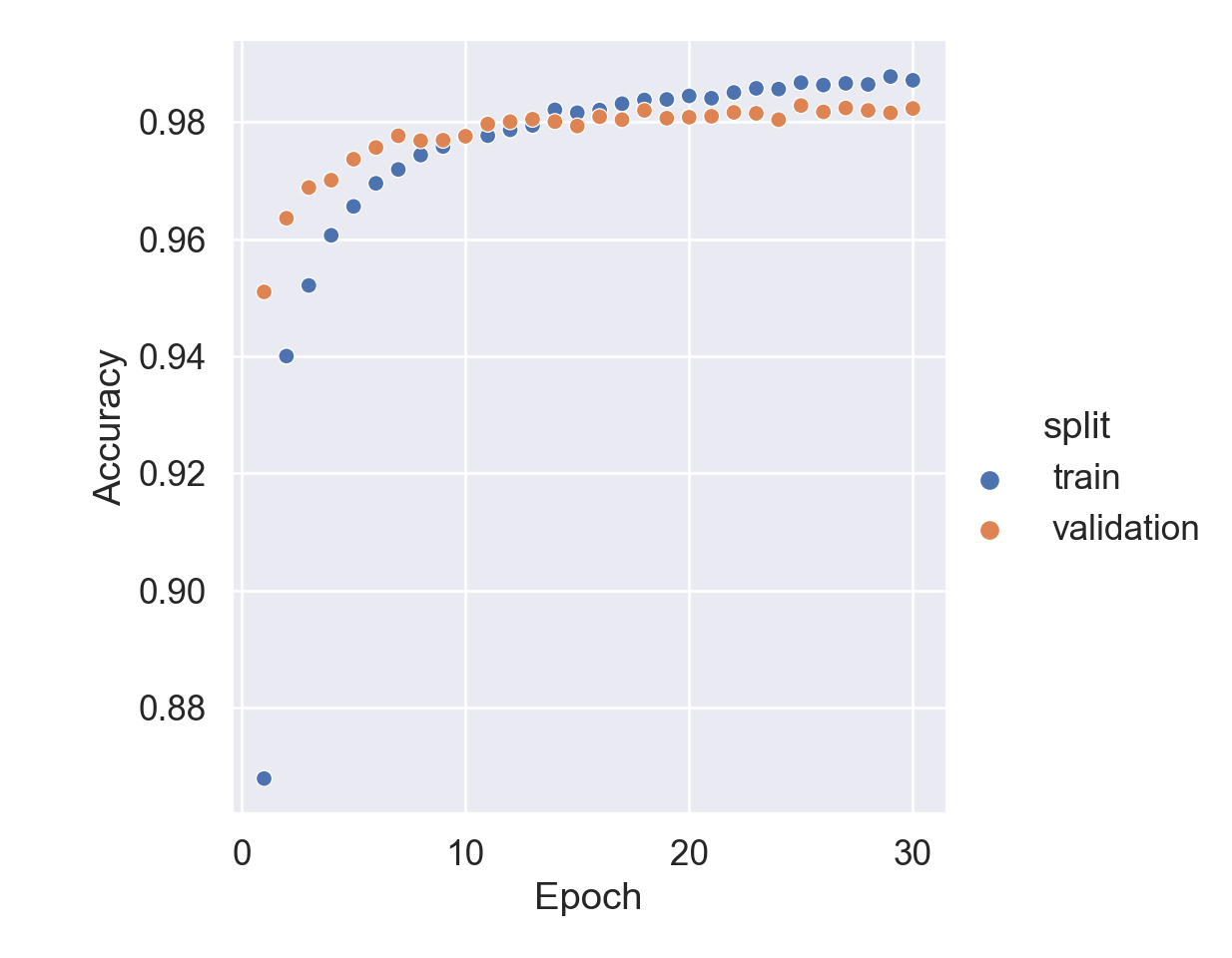
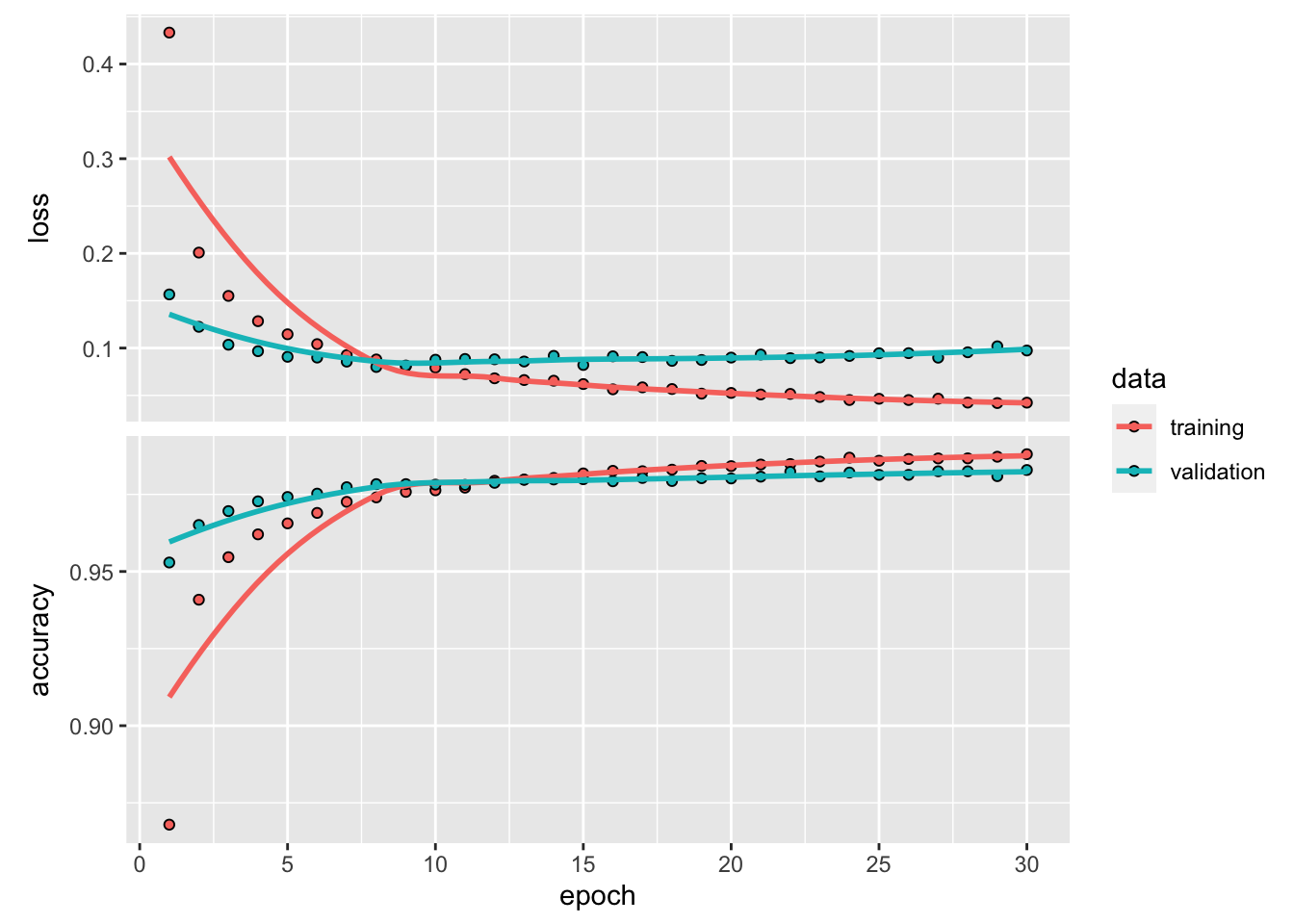
)Plot training history:
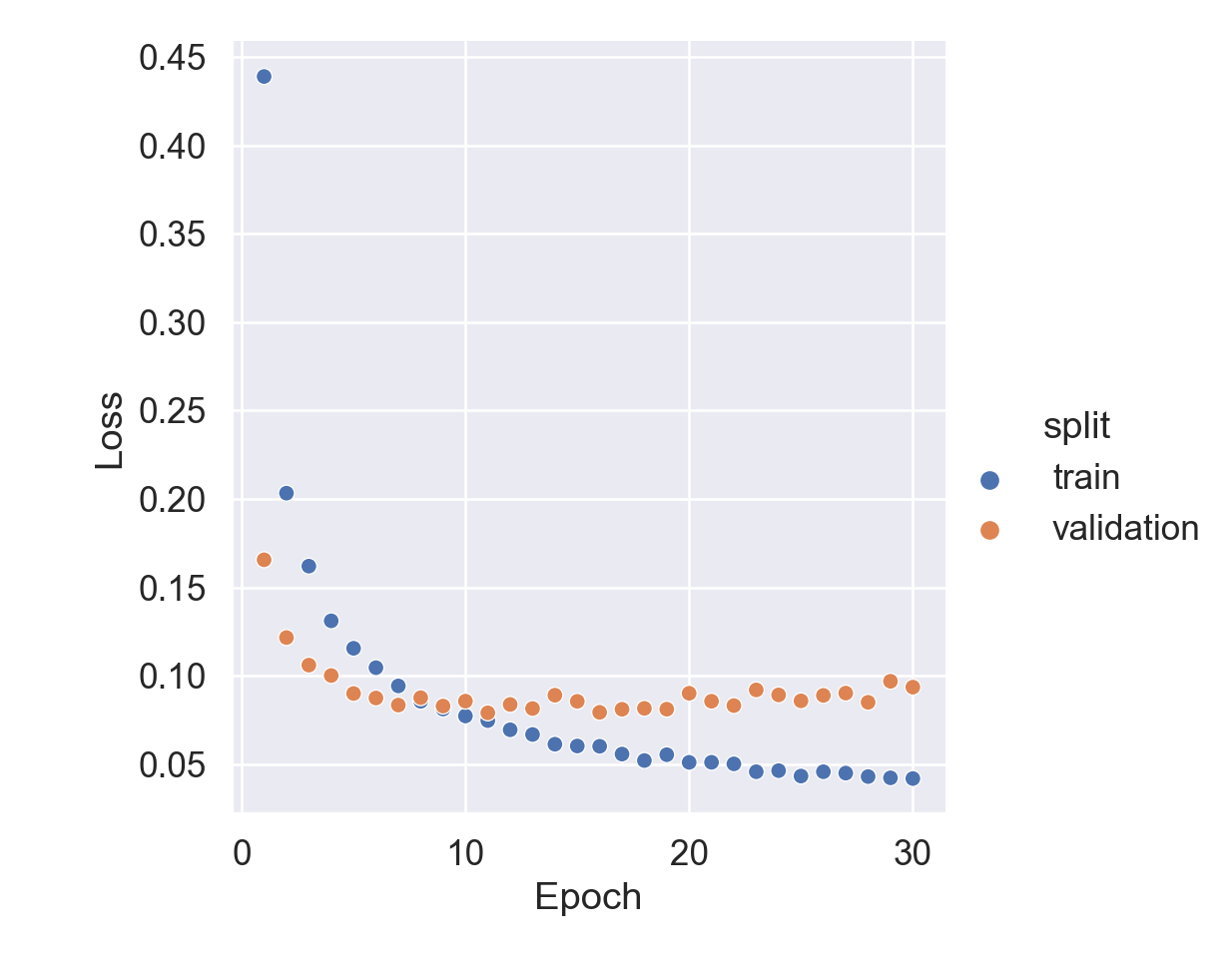
hist = pd.DataFrame(history.history)
hist['epoch'] = np.arange(1, epochs + 1)
hist = hist.melt(
id_vars = ['epoch'],
value_vars = ['loss', 'accuracy', 'val_loss', 'val_accuracy'],
var_name = 'type',
value_name = 'value'
)
hist['split'] = np.where(['val' in s for s in hist['type']], 'validation', 'train')
hist['metric'] = np.where(['loss' in s for s in hist['type']], 'loss', 'accuracy')
# Accuracy trace plot
plt.figure()
sns.relplot(
data = hist[hist['metric'] == 'accuracy'],
kind = 'scatter',
x = 'epoch',
y = 'value',
hue = 'split'
).set(
xlabel = 'Epoch',
ylabel = 'Accuracy'
);
plt.show()
# Loss trace plot
plt.figure()
sns.relplot(
data = hist[hist['metric'] == 'loss'],
kind = 'scatter',
x = 'epoch',
y = 'value',
hue = 'split'
).set(
xlabel = 'Epoch',
ylabel = 'Loss'
);
plt.show()
system.time({
history <- model %>% fit(
x_train, y_train,
epochs = 30, batch_size = 128,
validation_split = 0.2
)
}) user system elapsed
113.963 38.164 34.649 plot(history)
Evaluate model performance on the test data:
score = model.evaluate(x_test, y_test, verbose = 0)
print("Test loss:", score[0])Test loss: 0.08525163680315018print("Test accuracy:", score[1])Test accuracy: 0.9824000000953674model %>% evaluate(x_test, y_test) loss accuracy
0.08609481 0.98229998 Generate predictions on new data:
model %>% predict(x_test) %>% k_argmax()tf.Tensor([7 2 1 ... 4 5 6], shape=(10000), dtype=int64)Suppose we want to fit a multinomial-logit model and use it as a baseline method to neural networks. How to do that? Of course we can use mlogit or other packages. Instead we can fit the same model using keras, since multinomial-logit is just an MLP with (1) one input layer with linear activation and (2) one output layer with softmax link function.
# set up model
library(keras)
mlogit <- keras_model_sequential()
mlogit %>%
# layer_dense(units = 256, activation = 'linear', input_shape = c(784)) %>%
# layer_dropout(rate = 0.4) %>%
layer_dense(units = 10, activation = 'softmax', input_shape = c(784))
summary(mlogit)Model: "sequential_2"
________________________________________________________________________________
Layer (type) Output Shape Param #
================================================================================
dense_6 (Dense) (None, 10) 7850
================================================================================
Total params: 7,850
Trainable params: 7,850
Non-trainable params: 0
________________________________________________________________________________# compile model
mlogit %>% compile(
loss = 'categorical_crossentropy',
optimizer = optimizer_rmsprop(),
metrics = c('accuracy')
)
mlogitModel: "sequential_2"
________________________________________________________________________________
Layer (type) Output Shape Param #
================================================================================
dense_6 (Dense) (None, 10) 7850
================================================================================
Total params: 7,850
Trainable params: 7,850
Non-trainable params: 0
________________________________________________________________________________# fit model
mlogit_history <- mlogit %>%
fit(
x_train,
y_train,
epochs = 20,
batch_size = 128,
validation_split = 0.2
)# Evaluate model performance on the test data:
mlogit %>% evaluate(x_test, y_test) loss accuracy
0.2697336 0.9279000 Generate predictions on new data:
mlogit %>% predict(x_test) %>% k_argmax()tf.Tensor([7 2 1 ... 4 5 6], shape=(10000), dtype=int64)Experiment: Change the linear activation to relu in the multinomial-logit model and see the change in classification accuracy.